Remove duplicated items from an array
PROBLEM
The purpose of this post is to document and analyse the TIME efficiency of different implementations to remove duplicated items from an array.
CLARIFICATION
Optimizing a specific part of code should be considered when the impact on the overall program depends very much on how much time is actually spent in that specific fraction of code (Amdahl's law).
In the end, it is a matter of cost-benefit in combination with an exercise of performance analysis. The performance of a code section is a mix between frequency and efficiency:
How many times will your code be executed and how often? With what data will it be executed?Optimizations can be a two-edged sword! It can provide some time or space improvements but at the same time, you might be sacrificing readability, reliability, and programmer time which usually are far more important in the majority of cases. We should care only to spend time optimizing things that will make a difference.
This experiment doesn’t make sense with a small array of elements since the impact of the algorithm is negligible. In that kind of case, there are factors that will be more determinant than the algorithm itself. The most common overhead in that kind of application is the CPU workload, data transfer, memory, etc. These can affect drastically and add some randomness to the experiment. I’m not going to take any kind of theoretical approach. It’s purely experimental!
SOLUTION
To mesure the algorithm impact, we are going to introduce 2 variables: the array size (NUM_ELEMENTS) and the repetition rate (REPETITION_RATE).
const NUM_ELEMENTS = 10_000; // 10.000
const REPETITION_RATE = {
UNUSUAL: NUM_ELEMENTS * 1000,
CASUAL: NUM_ELEMENTS * 100,
LIKELY: NUM_ELEMENTS
};
The repetition rate is a pseudo-solution to introduce some duplicate elements with a higher or lower probability. To do so, I defined 3 repetition rate levels: LIKELY, CASUAL, and UNUSUAL, each repetition rate level has a different range of values that each array element can take.
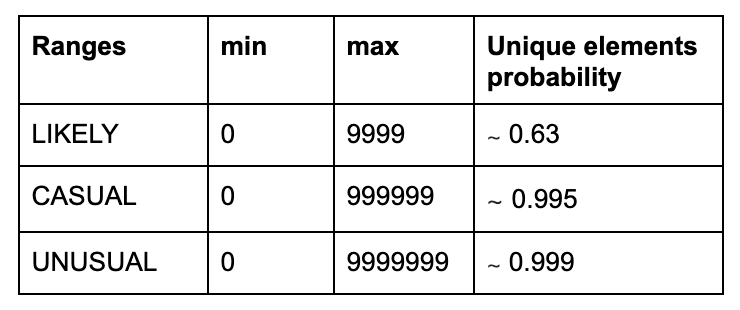
To calculate an array of NUM_ELEMENTS elements and fill it with random numbers between a defined range, I’m going to use the following function:
const data = (rate) => Array(NUM_ELEMENTS).fill().map(
() => Math.floor(Math.random() * REPETITION_RATE[rate])
);
Taking into account the previously mentioned, I’m going to present probably the most common and simple solutions to remove duplicated items from an array. For the sake of the simplicity, the experiment will be done over an array of numbers:
const withSet = (array) => {
return [...new Set(array)]
};
const withForLoop = (array) => {
var seen = {};
var out = [];
var len = array.length;
var j = 0;
for (var i = 0; i < len; i++) {
var item = array[i];
if (seen[item] !== 1) {
seen[item] = 1;
out[j++] = item;
}
}
return out;
}
const withSort = (array) => {
return array.sort().filter((item, i, self) => {
return !i || item != self[i - 1];
})
}
const withFilter = (array) => {
return array.filter((item, i, self) => {
return self.indexOf(item) == i
})
}
To ensure the empirical result, each algorithm is executed 10 times over the same dataset. To do so, I created a simple function to measure the execution time of each algorithm execution:
const calculate = (execute) => {
let init = performance.now();
execute();
let end = performance.now();
return end - init;
}
In order to be able to measure the impact of the algorithms, I will use a large enough array (NUN_ELEMENTS = 10.000).
Let’s analyze how many milliseconds take to execute each algorithm and represent it in a boxplot. You are able to check all the raw values in the Annex section.
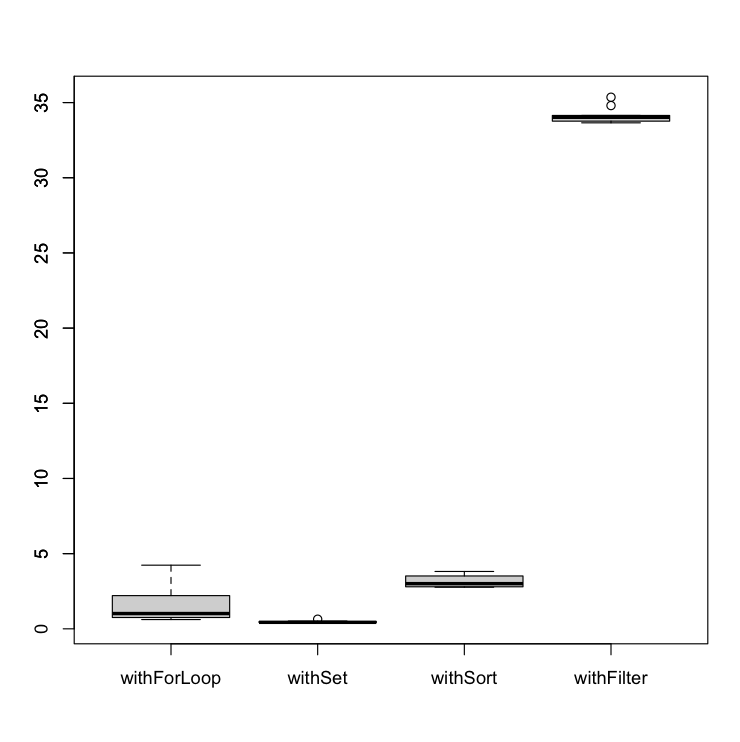
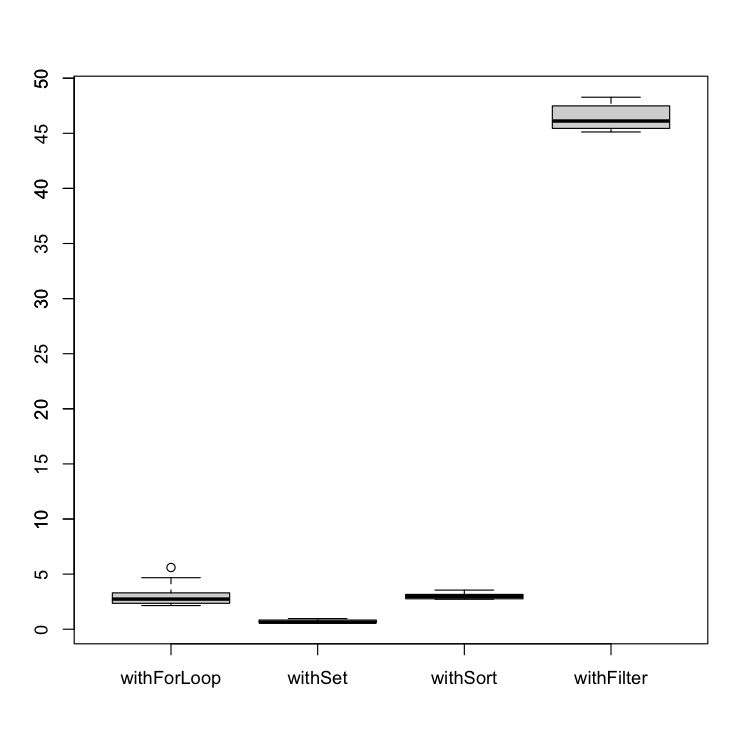
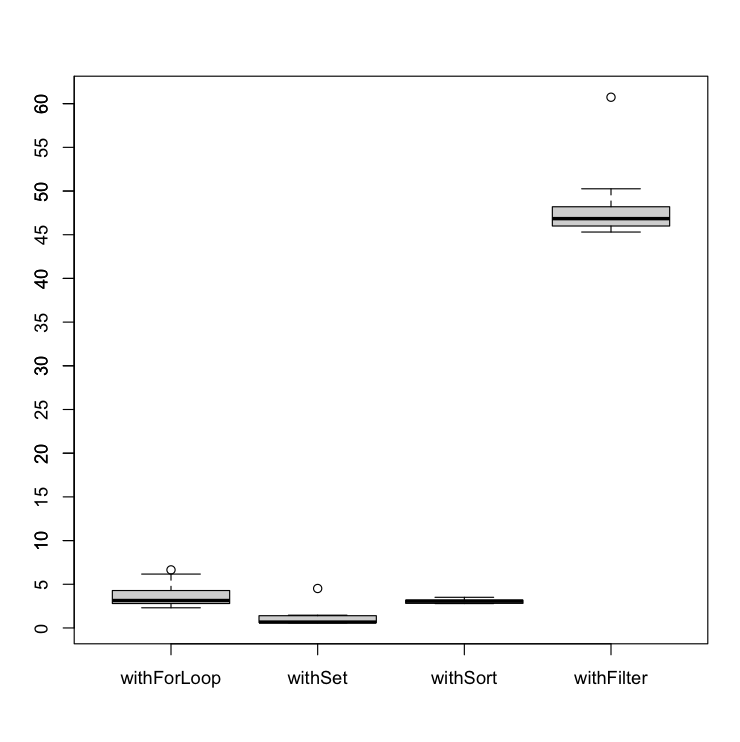
The worst algorithm so far is the withFilter. In addition, as could be seen, it is highly affected by the repetition rate. The withFilter performs much more better with a high number of repeated elements.
If we omit the results of the withFilter algorithm, we can dive into more detail in the results:
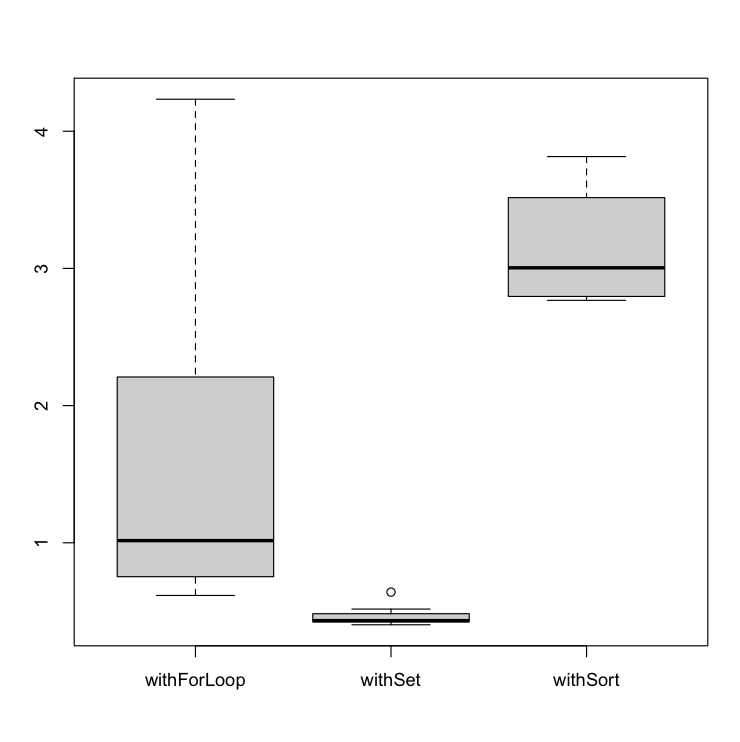
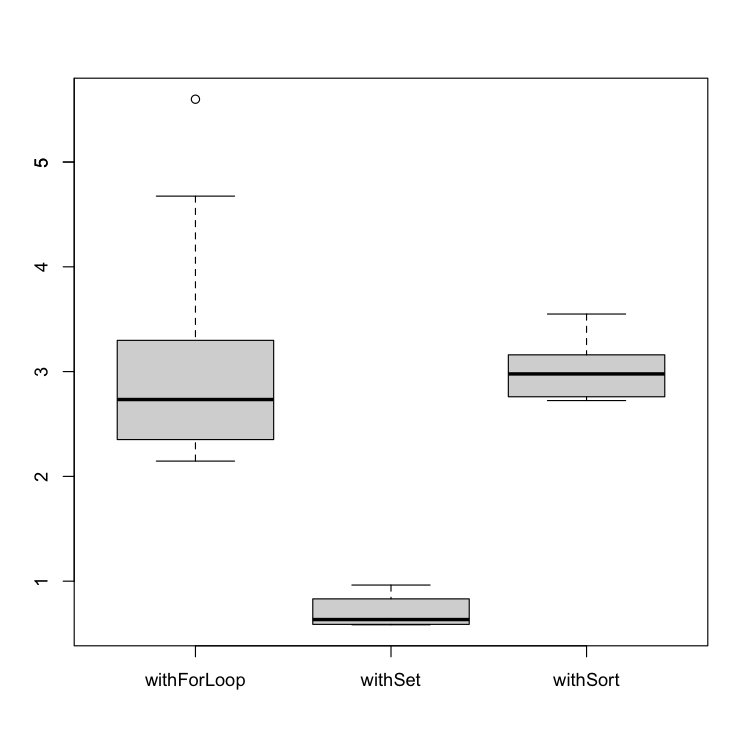
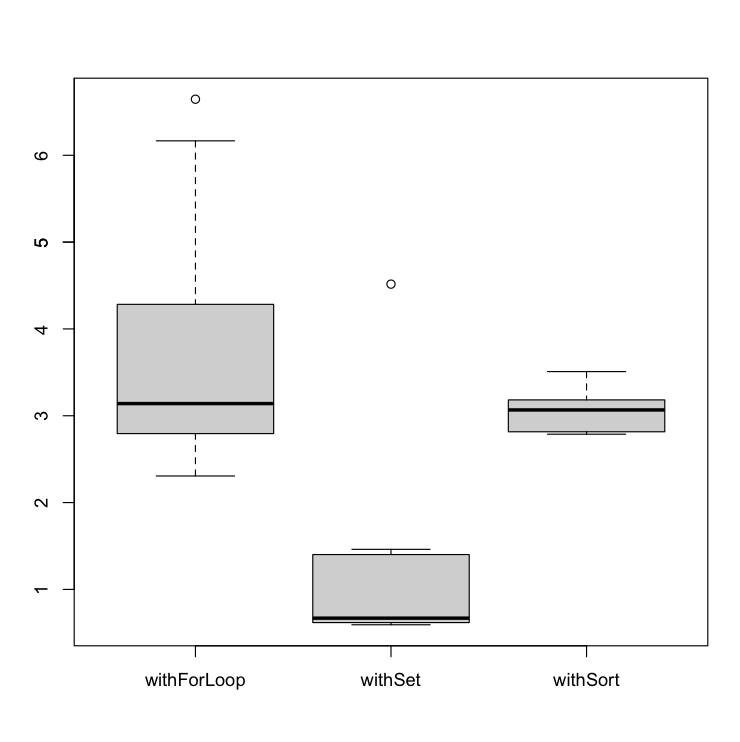
Independently of the repetition rate applied, the withSet performs much better than the other algorithms.
In addition, we can observe a correlation between the repetition rate and the performance of the withForLoop and withSet algorithms (as withFilter does).
Higher repetition rate ⇒ Better performance. Processing a new unique element has a higher cost than processing a duplicated element
For example, in the withForLoop algorithm, it can be easily guessed the extra work for each unique value:
// Duplicated?
if (seen[item] !== 1) {
// Add new unique element
seen[item] = 1;
out[j++] = item;
}
However, the withSort isn’t highly affected which makes sense.
What will happen if we apply the algorithms to 1 million elements (NUM_ELEMENTS = 1.000.000)?
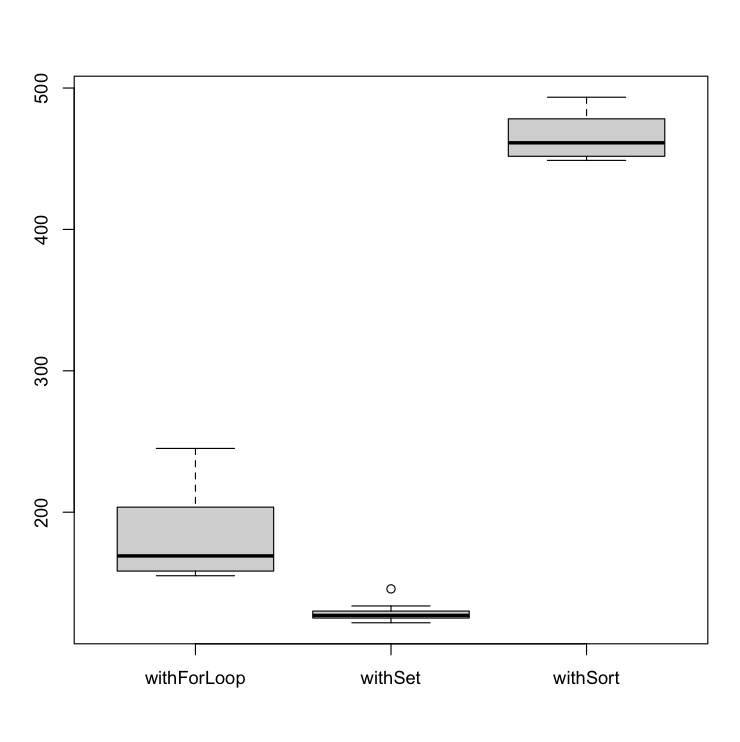
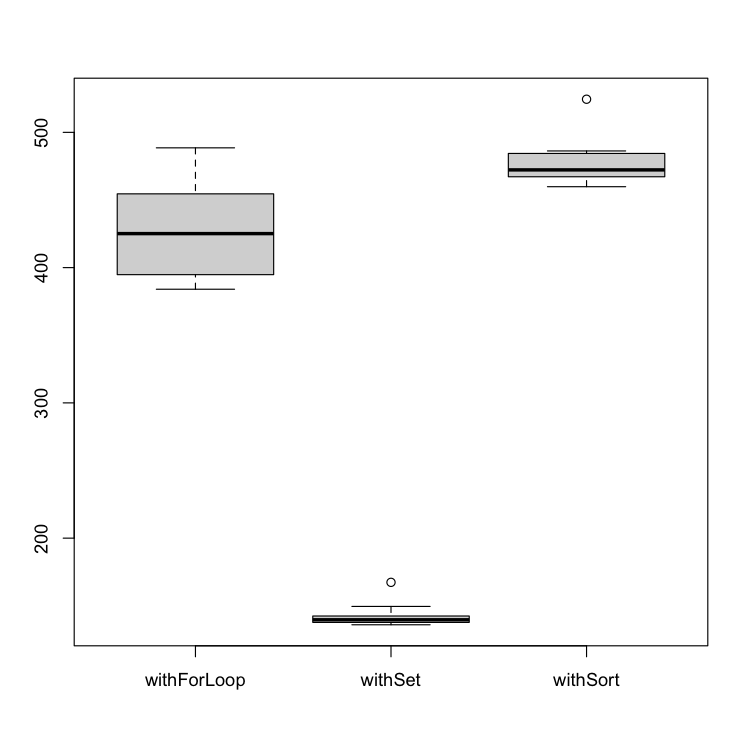
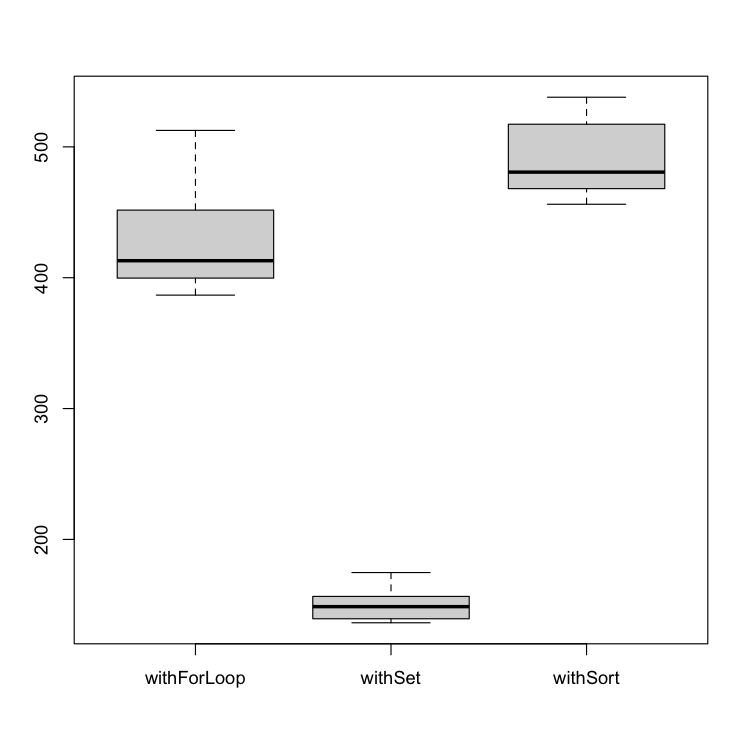
We can observe that the correlation is more evident when we apply the algorithms in a larger dataset. In a large enough dataset, the withSort algorithm is worst than the two remaining (withForLoop and withSet).
Even so, there is one scenario where the withSort method performs better than the others; when the given array is already sorted.
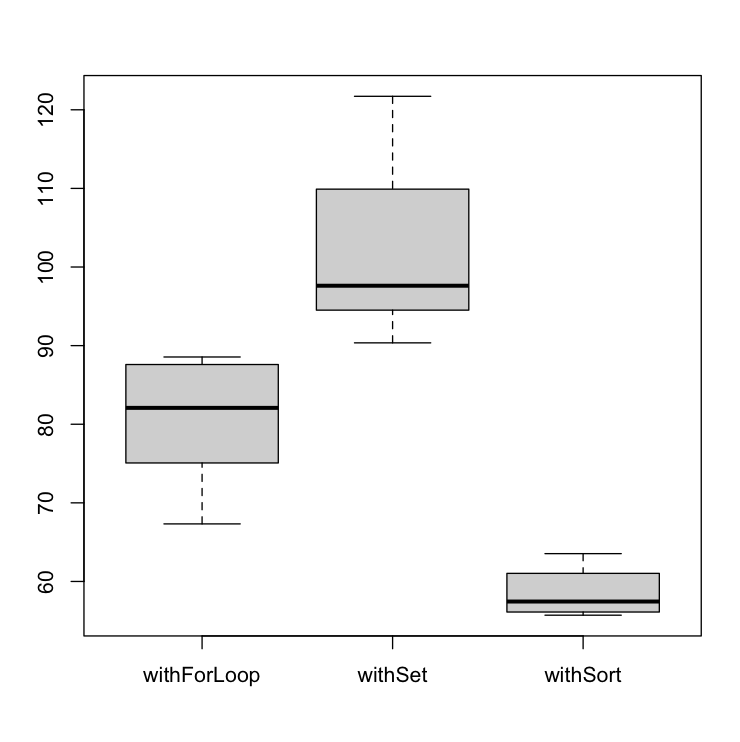
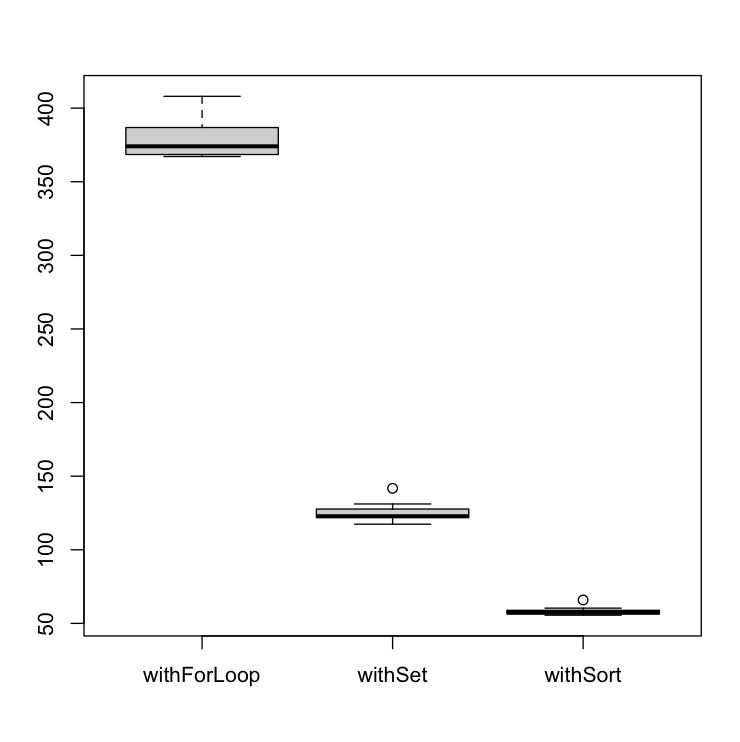
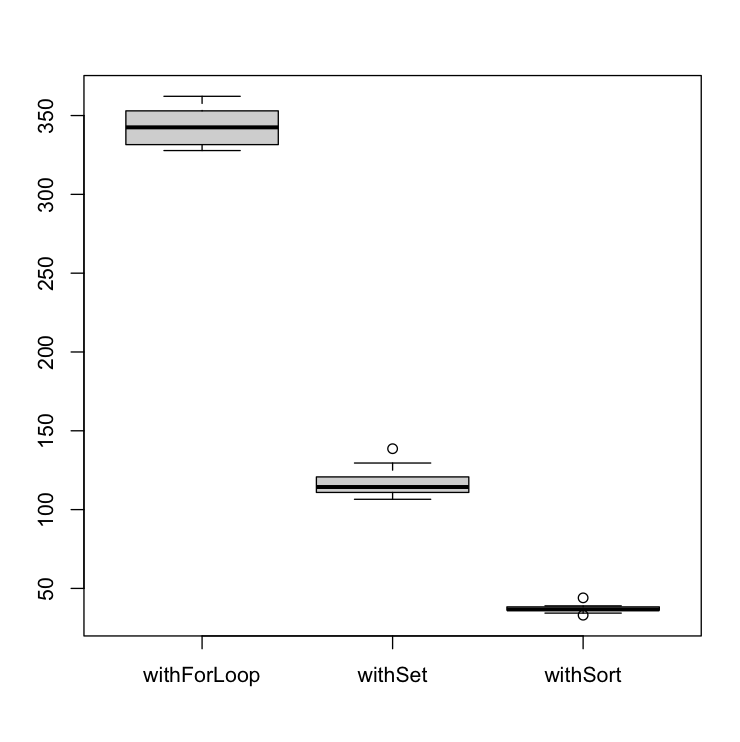
In addition, in this scenario, the withForLoop performs a little bit better than the withSet method when we have a high repetition rate. It appears to be related to branch prediction.
If we omit the results of the withSort algorithm, we can dive into more detail in the results. Even, if we ignore the sorted array scenario and keep the arbitrariness, what will happen if we apply the algorithms to 10 million elements (NUM_ELEMENTS = 10.000.000)? The correlation is even more evident in both algorithms.
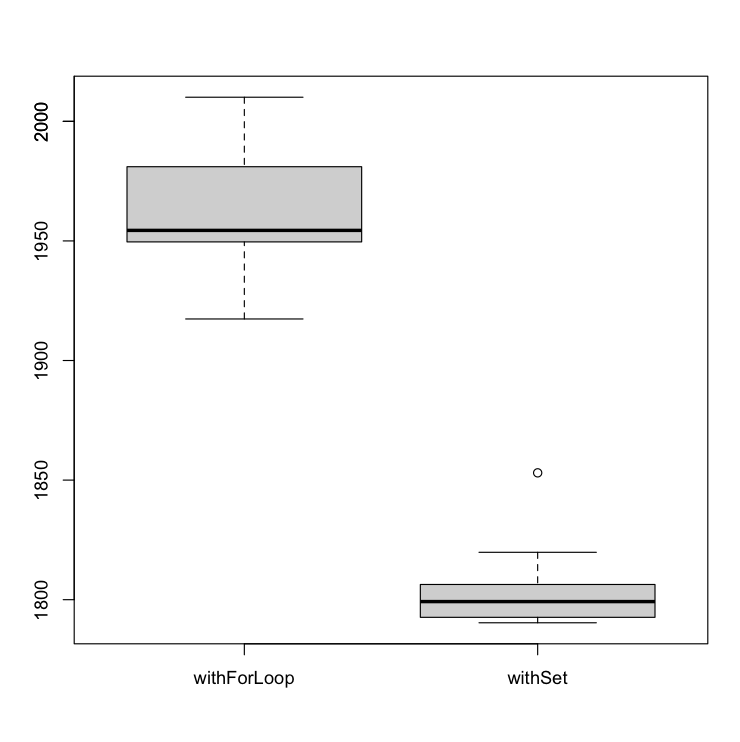
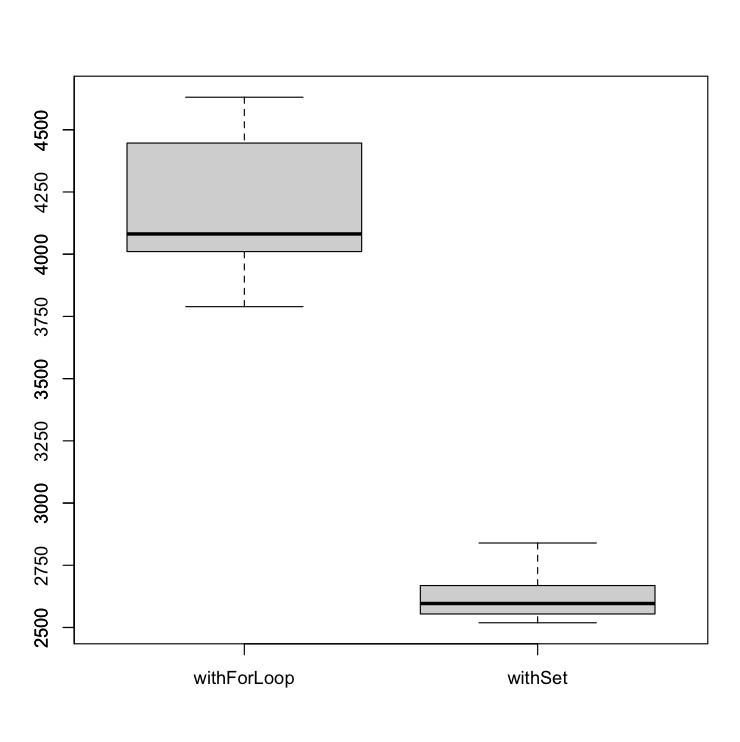
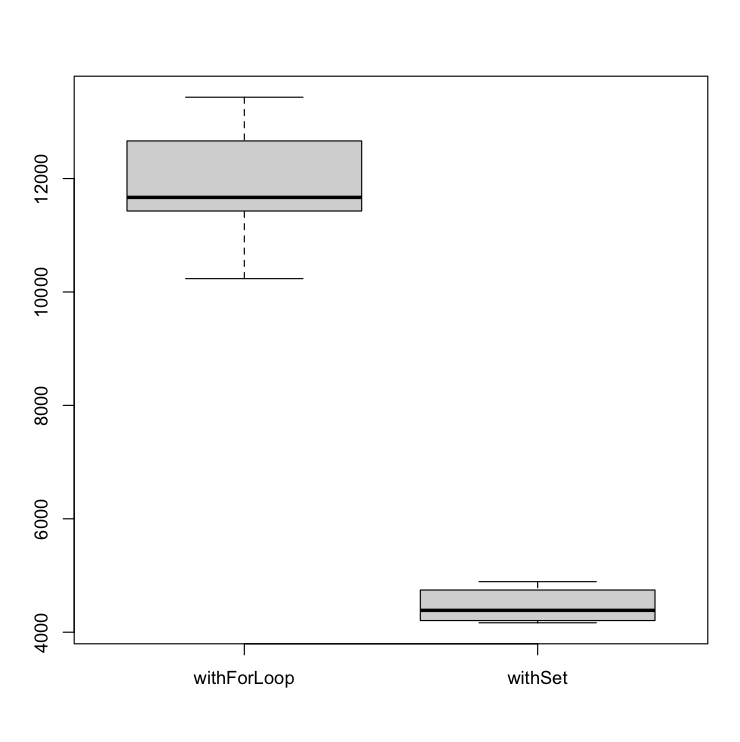
CONCLUSION
The best algorithm so far is the withSet. Luckily is the simpler and the most readable!
As I said, in the most common cases, you shouldn’t care about these micro-optimizations unless the algorithm is the core of your application. In the end, it’s a performance analysis exercise.
ANNEX
NUM_ELEMENTS = 10_000 - REPETITION_RATE = LIKELY
{
withForLoop: {
min: 0.6161800026893616,
max: 4.2332499995827675,
average: 1.553389500454068,
median: 1.015947999432683,
results: [
4.2332499995827675,
1.1240199990570545,
2.6671050004661083,
2.2087169997394085,
0.7861710004508495,
0.9078759998083115,
1.594580002129078,
0.6161800026893616,
0.642960000783205,
0.7530359998345375
]
},
withSet: {
min: 0.4024589993059635,
max: 0.6405039988458157,
average: 0.4619603998959064,
median: 0.4326910004019737,
results: [
0.48315799981355667,
0.43505600094795227,
0.4303259998559952,
0.4024589993059635,
0.6405039988458157,
0.453405000269413,
0.43005000054836273,
0.4045730009675026,
0.5168850012123585,
0.4231879971921444
]
},
withSort: {
min: 2.767271999269724,
max: 3.8152489997446537,
average: 3.165797100588679,
median: 3.0043945014476776,
results: [
3.8009399995207787,
3.5159769989550114,
2.9593700021505356,
2.9771270006895065,
3.199684999883175,
3.0316620022058487,
2.794938001781702,
2.767271999269724,
2.7957510016858578,
3.8152489997446537
]
},
withFilter: {
min: 33.65182099863887,
max: 35.35537299886346,
average: 34.15013259984553,
median: 34.02158449962735,
results: [
34.800221998244524,
35.35537299886346,
33.73582600057125,
33.99973299726844,
34.043436001986265,
34.06344199925661,
33.9438509978354,
33.76401100307703,
34.14361100271344,
33.65182099863887
]
}
}
NUM_ELEMENTS = 10_000 - REPETITION_RATE = CASUAL
{
withForLoop: {
min: 2.145897999405861,
max: 5.599513001739979,
average: 3.1290818996727467,
median: 2.733591500669718,
results: [
5.599513001739979,
2.9871659986674786,
4.6746309995651245,
2.351264998316765,
2.435266997665167,
2.145897999405861,
2.3316360004246235,
3.298259999603033,
2.9040569998323917,
2.563126001507044
]
},
withSet: {
min: 0.5837909989058971,
max: 0.9629179984331131,
average: 0.6997227989137172,
median: 0.6336345002055168,
results: [
0.6274590007960796,
0.8656079992651939,
0.7128149978816509,
0.5837909989058971,
0.5877099968492985,
0.9629179984331131,
0.6015109978616238,
0.639809999614954,
0.5845829993486404,
0.8310230001807213
]
},
withSort: {
min: 2.7234829999506474,
max: 3.549414001405239,
average: 2.9976361002773046,
median: 2.9778910018503666,
results: [
3.0144580006599426,
3.0532069988548756,
2.7598399966955185,
3.1632930003106594,
2.9413240030407906,
2.752921000123024,
2.7234829999506474,
2.8584109991788864,
3.549414001405239,
3.160010002553463
]
},
withFilter: {
min: 45.12157400324941,
max: 48.27394500002265,
average: 46.47778210006654,
median: 46.11468300037086,
results: [
48.27394500002265,
46.07310400158167,
45.861281000077724,
45.44522299990058,
45.12157400324941,
47.66389499977231,
45.37212799862027,
47.487910997122526,
47.32249800115824,
46.15626199916005
]
}
}
NUM_ELEMENTS = 10_000 - REPETITION_RATE = UNUSUAL
{
withForLoop: {
min: 2.3064499981701374,
max: 6.645658999681473,
average: 3.8001832999289036,
median: 3.140233000740409,
results: [
6.1662480011582375,
2.7944019995629787,
4.219734001904726,
2.8926009982824326,
4.283261999487877,
2.3064499981701374,
2.9883799999952316,
3.292086001485586,
2.413010999560356,
6.645658999681473
]
},
withSet: {
min: 0.5926219969987869,
max: 4.515944998711348,
average: 1.2056124992668629,
median: 0.6688965000212193,
results: [
0.6639479994773865,
1.4014370031654835,
4.515944998711348,
0.673845000565052,
0.6214400008320808,
0.8942089974880219,
0.6134370006620884,
0.617748998105526,
0.5926219969987869,
1.4614929966628551
]
},
withSort: {
min: 2.7875970005989075,
max: 3.5085639990866184,
average: 3.068043800070882,
median: 3.0669784992933273,
results: [
3.1199680007994175,
3.5085639990866184,
2.927454002201557,
3.3949429988861084,
2.795676000416279,
2.815430000424385,
2.7875970005989075,
3.134131997823715,
3.013988997787237,
3.182685002684593
]
},
withFilter: {
min: 45.30747600272298,
max: 60.73564099892974,
average: 48.38645560033619,
median: 46.84241000004113,
results: [
60.73564099892974,
47.12230399996042,
46.28296400234103,
45.34110099822283,
45.996991001069546,
45.30747600272298,
46.56251600012183,
48.059397000819445,
48.20021599903703,
50.25595000013709
]
}
}
NUM_ELEMENTS = 1_000_000 - REPETITION_RATE = LIKELY
{
withForLoop: {
min: 155.05746100097895,
max: 245.10848499834538,
average: 181.6651143990457,
median: 169.08007649704814,
results: [
203.5708300024271,
161.23485799878836,
155.05746100097895,
170.27531999349594,
157.80864299833775,
225.59701199829578,
245.10848499834538,
171.7655059993267,
167.88483300060034,
158.34819599986076
]
},
withSet: {
min: 121.78685899823904,
max: 145.75340899825096,
average: 128.705806799978,
median: 127.01133299991488,
results: [
127.67670299857855,
126.34596300125122,
122.60724800080061,
125.9666019976139,
121.78685899823904,
130.07025100290775,
145.75340899825096,
133.6826130002737,
125.13346000015736,
128.03496000170708
]
},
withSort: {
min: 448.8328679949045,
max: 493.5059050023556,
average: 465.22751189991834,
median: 461.2731125019491,
results: [
448.8328679949045,
466.63669400662184,
464.6501320004463,
449.6672699972987,
493.5059050023556,
457.8960930034518,
451.7257089987397,
489.2764909937978,
451.85943400114775,
478.22452300041914
]
}
}
NUM_ELEMENTS = 1_000_000 - REPETITION_RATE = CASUAL
{
withForLoop: {
min: 384.021381996572,
max: 488.5499190017581,
average: 427.4536935999989,
median: 425.1403129994869,
results: [
394.7962369993329,
408.4729050025344,
413.82565400004387,
450.74423100054264,
455.4311800003052,
436.45497199893,
488.5499190017581,
384.021381996572,
387.7007130011916,
454.5397429987788
]
},
withSet: {
min: 135.95582000166178,
max: 167.32689300179482,
average: 142.8933510005474,
median: 139.64554500207305,
results: [
137.69809199869633,
141.28855700045824,
138.00253300368786,
137.7896299958229,
142.44284000247717,
141.87754200398922,
167.32689300179482,
149.52464500069618,
135.95582000166178,
137.0269579961896
]
},
withSort: {
min: 459.81696800142527,
max: 524.4922409951687,
average: 478.2014821983874,
median: 472.2513504959643,
results: [
459.81696800142527,
524.4922409951687,
470.29814099520445,
474.20455999672413,
486.25255700200796,
461.06839399784803,
467.16533199697733,
470.1375120058656,
484.4119429960847,
484.1671739965677
]
}
}
NUM_ELEMENTS = 1_000_000 - REPETITION_RATE = UNUSUAL
{
withForLoop: {
min: 386.68828999996185,
max: 512.5664549991488,
average: 424.4509158007801,
median: 412.9922320023179,
results: [
387.05061000585556,
386.68828999996185,
451.6580500006676,
512.5664549991488,
423.45554799586535,
407.7165110036731,
457.4781470000744,
399.9279880002141,
399.6996060013771,
418.26795300096273
]
},
withSet: {
min: 136.28456499427557,
max: 174.66381999850273,
average: 150.22565199807286,
median: 148.61589350178838,
results: [
153.5806260034442,
161.41218699514866,
143.65116100013256,
136.28456499427557,
143.53657999634743,
139.3451649993658,
174.66381999850273,
156.44387900084257,
155.3550329953432,
137.9835039973259
]
},
withSort: {
min: 456.1394260004163,
max: 537.935175999999,
average: 488.6582931995392,
median: 480.69253949820995,
results: [
473.29733599722385,
517.2986389994621,
456.1394260004163,
537.935175999999,
517.5273750051856,
468.0702169984579,
461.11141999810934,
493.8182640001178,
479.4086980000138,
481.9763809964061
]
}
}
NUM_ELEMENTS = 1_000_000 - REPETITION_RATE = LIKELY - PRESORTED
{
withForLoop: {
min: 67.32201500236988,
max: 88.55460099875927,
average: 80.63559990078211,
median: 82.08199950307608,
results: [
88.55460099875927,
81.92778299748898,
87.59654499590397,
84.62078499794006,
88.41655300557613,
82.23621600866318,
69.48410500586033,
67.32201500236988,
75.0740189999342,
81.12337699532509
]
},
withSet: {
min: 90.35226999223232,
max: 121.71554899215698,
average: 101.35781189799309,
median: 97.61934300512075,
results: [
121.71554899215698,
100.78924599289894,
93.27231799066067,
94.89483200013638,
94.51389099657536,
112.895673006773,
109.90565399825573,
97.37541399896145,
90.35226999223232,
97.86327201128006
]
},
withSort: {
min: 55.708606988191605,
max: 63.539028003811836,
average: 58.58115369826555,
median: 57.44712050259113,
results: [
57.8816349953413,
57.012606009840965,
62.98825399577618,
55.708606988191605,
56.07959200441837,
56.68088099360466,
58.779587000608444,
61.02952899038792,
56.11181800067425,
63.539028003811836
]
}
}
NUM_ELEMENTS = 1_000_000 - REPETITION_RATE = CASUAL - PRESORTED
{
withForLoop: {
min: 367.14336800575256,
max: 408.04874999821186,
average: 379.1356734991074,
median: 374.08505799621344,
results: [
408.04874999821186,
385.46425899863243,
386.83866499364376,
389.89311300218105,
368.5118200033903,
375.32072000205517,
369.17063499987125,
372.8493959903717,
368.1160089969635,
367.14336800575256
]
},
withSet: {
min: 117.38054099678993,
max: 141.73810701072216,
average: 125.5299181997776,
median: 122.77016250044107,
results: [
141.73810701072216,
121.27236399054527,
122.01307900249958,
121.94323199987411,
122.74919401109219,
131.10868400335312,
117.38054099678993,
126.6241319924593,
127.6787180006504,
122.79113098978996
]
},
withSort: {
min: 55.56011998653412,
max: 65.89031200110912,
average: 58.22068350017071,
median: 57.26997400075197,
results: [
60.35952399671078,
57.611115008592606,
56.768538013100624,
57.54646299779415,
58.87953099608421,
65.89031200110912,
55.56011998653412,
56.99348500370979,
56.1416649967432,
56.45608200132847
]
}
}
NUM_ELEMENTS = 1_000_000 - REPETITION_RATE = UNUSUAL - PRESORTED
{
withForLoop: {
min: 327.7845759987831,
max: 362.2078289985657,
average: 342.5873847991228,
median: 342.51240300387144,
results: [
336.3179539889097,
355.4238319993019,
346.7273070067167,
327.7845759987831,
362.2078289985657,
344.6583460122347,
327.86210499703884,
331.5532739907503,
340.3664599955082,
352.9721650034189
]
},
withSet: {
min: 106.5443020015955,
max: 138.63980700075626,
average: 117.35592220425606,
median: 114.33523450791836,
results: [
110.89038001000881,
108.69839200377464,
129.5499380081892,
138.63980700075626,
106.5443020015955,
114.91061700880527,
118.87106600403786,
120.74676299095154,
110.94810500741005,
113.75985200703144
]
},
withSort: {
min: 33.01224599778652,
max: 44.01350799202919,
average: 37.149842695891856,
median: 36.649998001754284,
results: [
36.47280099987984,
36.19507499039173,
36.40855699777603,
44.01350799202919,
36.82719500362873,
37.01220999658108,
38.938134998083115,
33.01224599778652,
34.333357989788055,
38.28534199297428
]
}
}
NUM_ELEMENTS = 10_000_000 - REPETITION_RATE = LIKELY
{
withForLoop: {
min: 1917.3692060038447,
max: 2010.0801389962435,
average: 1962.0589136004448,
median: 1954.4033880010247,
results: [
2010.0801389962435,
1917.3692060038447,
1959.8589759990573,
1949.5907730013132,
1956.6235629990697,
1952.1832130029798,
1981.0251489952207,
1951.4385790005326,
1994.0854310020804,
1948.334107004106
]
},
withSet: {
min: 1790.3471409976482,
max: 1853.03464499861,
average: 1805.2915181994438,
median: 1799.2067870013416,
results: [
1819.8134460002184,
1805.9403330013156,
1806.3639229983091,
1795.3301180005074,
1790.3471409976482,
1795.9115020036697,
1791.045364998281,
1792.6266369968653,
1853.03464499861,
1802.5020719990134
]
}
}
NUM_ELEMENTS = 10_000_000 - REPETITION_RATE = CASUAL
{
withForLoop: {
min: 3789.1354789957404,
max: 4630.735077001154,
average: 4178.7110580004755,
median: 4081.3821364976466,
results: [
3789.1354789957404,
4028.857537999749,
4010.4580660015345,
4574.977958001196,
4630.735077001154,
4160.151626005769,
3983.446921005845,
4065.9210390001535,
4096.84323399514,
4446.58364199847
]
},
withSet: {
min: 2518.947176001966,
max: 2839.48312599957,
average: 2616.3203426986934,
median: 2596.4002064988017,
results: [
2668.5661209970713,
2687.6818829998374,
2589.4644069969654,
2519.6772719994187,
2603.336006000638,
2839.48312599957,
2607.236534997821,
2554.2970929965377,
2574.5138079971075,
2518.947176001966
]
}
}
NUM_ELEMENTS = 10_000_000 - REPETITION_RATE = UNUSUAL
{
withForLoop: {
min: 10235.086987003684,
max: 13434.179785996675,
average: 11923.496706897766,
median: 11667.779426496476,
results: [
10235.086987003684,
12663.538829997182,
11813.862790994346,
11065.280889995396,
11427.339896000922,
11521.696061998606,
11503.277909994125,
13021.919983997941,
13434.179785996675,
12548.783932998776
]
},
withSet: {
min: 4166.4050879999995,
max: 4891.42372700572,
average: 4458.152116901428,
median: 4385.465481501073,
results: [
4308.565682001412,
4891.42372700572,
4195.092826999724,
4806.711855001748,
4205.6086410060525,
4744.175035998225,
4258.800287000835,
4462.365281000733,
4166.4050879999995,
4542.372744999826
]
}
}